Given six cities and the costs(in millions of dollars) of rebuilding roads between them. The road commission has decided to rebuild enough roads so that each pair of cities will be connected, either directly or by going through other cities, by rebuilt roads. Find a minimum cost set of roads meeting its criterion.
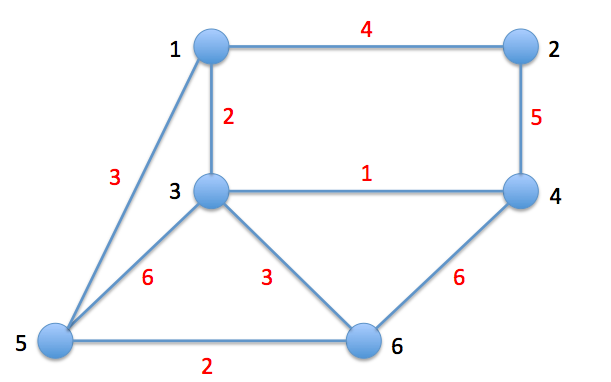
We visited this question previously with Kruskal’s Algorithm. Now let’s try a different approach using Prim’s Algorithm.
Prim’s algorithm is another greedy algorithm that finds a minimal spanning tree in a connected, weighted graph. Unlike Kruskal’s algorithm, whose partial solutions are not necessarily connected, a partial solution in prim’s algorithm is a tree. Prim’s algorithm begins with a start vertex and no edges and then applies the greedy rule: Add an edge of minimum weight that has one vertex in the current tree and the other not in the current tree.
The big idea is to maintain a table that stores each vertex with its corresponding edge weight value adjacent to the starting vertex in question. Additionally, we need an array to store the ‘parent’ vertex that has access to the vertex in question. We then go about selecting the least weight value in the table and select it as the edge path to pick. The symbol for choosing this edge could be deleting the row entirely from the table. After each edge selection, we update the table with the newly accessible vertex. When there are no more rows left in the table, then we would have selected every edge required of a minimum spanning tree.
For the table above, we can use a python dictionary with key as the vertex and value as the edge weight with its ‘parent’ vertex.
We also require a container to store the vertices each vertex is able to reach directly. For this container, we can use an adjacency list. adj[i] is a reference to the first node in a linked list of nodes representing the vertices adjacent to vertex i. Here’s the adjacency list implementation:
class Node:
"""
Node class defines the basic structure of a node.
"""
def __init__(self, vertex=None, weight=None, next=None):
self.vertex = vertex
self.weight = weight
self.next = next
class LinkedList:
"""
LinkedList class defines a linked list of nodes in which node.next reference the next node in the list
"""
def __init__(self):
self.head = Node()
def get_head(self):
"""
Returns a reference to the head node
"""
return self.head
def add(self, vertex, weight):
"""
Append a new node with node.vertex as vertex to the last element in the linked list
"""
new_node = Node(vertex, weight)
trav = self.head
while(trav.next != None):
trav = trav.next
trav.next = new_node
def print_list(self):
trav = self.head.next
while trav != None:
print "(%d, %d)" % (trav.vertex, trav.weight),
trav = trav.next
By calling the function adj_list.print_list() method, we should get the following printout, which is the content of each adjacent node in the list.
(2, 4) (3, 2) (5, 3) None
(1, 4) (4, 5) None
(1, 2) (5, 6) (6, 3) (4, 1) None
(2, 5) (3, 1) (6, 6) None
(1, 3) (3, 6) (6, 2) None
(5, 2) (3, 3) (4, 6) None
Next, we define an Edges class to contain the table mentioned earlier. The class has a 2d list attribute like the following:
edges = [[vertex, weight, parent_vertex],...]
Each row of the table is represented by edges[i].
Edges class has the following attributes and methods:
class Edges:
"""
Edge table consisting of vertex, weight and parent_vertex in a row.
"""
edge_table = []
def __init__(self, adj_ref, start):
while adj_ref != None:
self.edge_table.append([adj_ref.vertex, adj_ref.weight, start])
adj_ref = adj_ref.next
def get_table(self):
return self.edge_table
def add_row(self, vertex, weight, parent_vertex):
"""
Add a row in table with vertex, weight and parent_vertex attributes
"""
self.edge_table.append([vertex, weight, parent_vertex])
def pop_row(self):
"""
Delete the row in table with the smallest weight and return the corresponding vertex.
"""
if len(self.edge_table) > 0:
least_weight = self.edge_table[0][1]
least_weight_index = 0
for i in range(1, len(self.edge_table)):
if self.edge_table[i][1] < least_weight:
least_weight = self.edge_table[i][1]
least_weight_index = i
least_weight_vertex = self.edge_table[least_weight_index][0]
self.edge_table.pop(least_weight_index)
return least_weight_vertex
else:
return None
def is_in(self, vertex):
"""
Return true if vertex is in table and false otherwise.
"""
for edge in self.edge_table:
if edge[0] == vertex:
return True
return False
def vertex_weight(self, vertex):
"""
Return the weight corresponding to vertex.
"""
for edge in self.edge_table:
if edge[0] == vertex:
return edge[1]
return None
def update_row(self, vertex, weight, parent_vertex):
"""
Changes the weight and parent_vertex corresponding to existing vertex.
"""
for edge in self.edge_table:
if edge[0] == vertex:
edge[1] = weight
edge[2] = parent_vertex
def print_table(self):
"""
Print edge_table.
"""
print self.edge_table
Lastly, we have our prim’s algorithm to sort out the minimum spanning tree of the directed, weighted graph.
def prim(adj_ref, start):
"""
Finds a minimal spanning tree in a connected, weighted, n-vertex graph.
The graph is represented using adjacency lists; adj[i] is a reference to the first node in a linked list of nodes.
The start vertex is start. In the minial spanning tree, the parent of a vertex is defined as the vertex where existing minimal tree vertex extends from.
Start vertex(parent of itself) is = 0.
"""
table = Edges(adj_ref[4].next, start)
chosen = []
chosen.append(start)
while len(table.get_table()) > 0:
table.print_table()
ver = table.pop_row()
chosen.append(ver)
print "Child vertex %d chosen." % ver
trav = adj_ref[ver].next
while trav != None:
if trav.vertex in chosen:
trav = trav.next
continue
if trav.vertex == start:
trav = trav.next
continue
if table.is_in(trav.vertex): # table has vertex
if trav.weight < table.vertex_weight(trav.vertex): # new edge weight is less than existing table value
table.update_row(trav.vertex, trav.weight, ver) # update table to new vertex and weight
else:
# insert vertex and its elements into table
table.add_row(trav.vertex, trav.weight, ver)
trav = trav.next
print chosen
The function prim is module level function and uses both Edges and LinkList classes to maintain interity and coherence of data.
It’s time to test the program:
if __name__ == "__main__":
adj_list = [0] * 6 # an array of adjacency list instances
adj = copy.deepcopy(adj_list) # references to head node
for i in range(len(adj_list)):
adj_list[i] = LinkedList() # declare linked list instance
adj[i] = adj_list[i].get_head() # reference adj[i] to head node
# Setup the adjacency list
adj_list[0].add(1,4)
adj_list[0].add(2,2)
adj_list[0].add(4,3)
adj_list[1].add(0,4)
adj_list[1].add(3,5)
adj_list[2].add(0,2)
adj_list[2].add(4,6)
adj_list[2].add(5,3)
adj_list[2].add(3,1)
adj_list[3].add(1,5)
adj_list[3].add(2,1)
adj_list[3].add(5,6)
adj_list[4].add(0,3)
adj_list[4].add(2,6)
adj_list[4].add(5,2)
adj_list[5].add(4,2)
adj_list[5].add(2,3)
adj_list[5].add(3,6)
prim(adj, 4)
With the last line prim(adj,4), the output would be:
[[0, 3, 4], [2, 6, 4], [5, 2, 4]]
Child vertex 5 chosen.
[[0, 3, 4], [2, 3, 5], [3, 6, 5]]
Child vertex 0 chosen.
[[2, 2, 0], [3, 6, 5], [1, 4, 0]]
Child vertex 2 chosen.
[[3, 1, 2], [1, 4, 0]]
Child vertex 3 chosen.
[[1, 4, 0]]
Child vertex 1 chosen.
[4, 5, 0, 2, 3, 1]
Okok some explaination on the output here, Every successive 2 lines indicates a successful selection of a vertex to be chosen as part of the minimal spanning tree. Each of the first line of 2d lists indicates the available options in the table. Second line, Child vertex x chosen. indicates which of the vertex(and its corresponding row) is chosen. The last line outputs the order of which the vertices are selected, with the first element being the start vertex.
Prim’s algorithm is also an optimal implementation of the greedy algorithm to achieve a minimal spanning tree. However, through repeated runtime tests, it seems Prim’s algorithm is consistently faster than Kruskal’s Algorithm. I did a time complexity analysis of Prim’s and came up with the following:
Prim’s algorithm time complexity(major functions):
**Operation** **Worst-Case Time**
Edges(adj_ref, start) O(n)
pop_row() O(lg n)
is_in(vertex) O(1)
vertex_weight(vertex) O(n)
update_row(vertex, weight, ..) O(n)
The outer while loop take time O(n). The inner loop has a relation with the number of edges. Since we know that given n vertices, there can be a maximum of 2n edges so the time complexity of the inner while loop has complexity of O(n**2).
So the final time complexity of prim’s algorithm will be O(n**3). This is a bad time complexity given that the operations are not very convoluted. I think the bottleneck of this implementation is the abstract data structure used. I used a linked list data structure which in itself has a complexity of O(n). If we can use a more efficient data structure such as binary minheap structure which has O(lg n) complexity, we can really reduce the time complexity of Prim’s algorithm to O(n2 lg n ). Maybe i’ll try to implement a binary minheap structure later.
Here’s my full implementation. I would love to hear suggestions on how to improve the time complexity or anything in general. Cheers :)
